Quantum Kata (1) - Basic Gates

Recently, I found QuantumKata which is a series of quantum programming questions that teaches the concept of quantum computing. The programming language used in this repository is Q# released by Microsoft. Although the repo claims itself as a tutorial, I find it lacks of explainations on the concept. If you are completly new to quantum computing, I would suggest to first go over the Quantum Quest lecture notes (super helpful!) then come back to these katas.

This blog series will record my solution to the katas in each section. This first post is going to be focusing on basic gates. Questions with a star beside the title means it is slightly challenging to solve. Since Q# is new to me and might be new to you, it would be better to keep the docs around. The namespace which will be referencing a lot in this post is intrinsic.

Part I. Single-Qubit Gates

Task 1.1 State flip: \(\left| 0 \right>\) to \(\left| 1 \right>\) and vice versa

Input: A qubit in state \(α \left| 0 \right> + β \left| 1 \right>\)

Goal: Change the state of the qubit to \(α \left| 1 \right> + β \left| 0 \right>\)

This question asks us to flip the qubit state, just like the not gate in classical computer. We can solve it easily by the X gate. It actually provides the solution in the comments.

operation StateFlip (q : Qubit) : Unit {
    body (...) {
        X(q);
    }
    adjoint self;
}

Task 1.2 Basis change: \(\left| 0 \right>\) to \(\left| + \right>\) and \(\left| 1 \right>\) to \(\left| - \right>\)

Input: A qubit in state \(α \left| 0 \right> + β \left| 1 \right>\)

Goal: Change the state of the qubit as follows:

If the qubit is in state \(\left| 0 \right>\), change its state to \(|+⟩ = \frac{\left| 0 \right> + \left| 1 \right>}{\sqrt{2}}\)

If the qubit is in state \(\left| 1 \right>\), change its state to \(|-⟩ = \frac{\left| 0 \right> - \left| 1 \right>}{\sqrt{2}}\)

If you did go over the quantum quest notes, this question is a no brainer. Hadamard (H) gate does exactly what the question asks. Also the inverse of Hadmard gate is itself, applying it twice will give us the original input.

operation BasisChange (q : Qubit) : Unit {
    body (...) {
        H(q);
    }
    adjoint self;
}

Task 1.3 Sign flip: \(\left| + \right>\) to \(\left| - \right>\) and vice versa

Input: A qubit in state \(α \left| 0 \right> + β \left| 1 \right>\)

Goal: Change the qubit state to \(α \left| 0 \right> - β \left| 1 \right>\)

Z gates will add a minus sign if the state is \(\left| 1 \right>\) and leave \(\left| 0 \right>\) unchanged. Perfect gate for this kata.

operation SignFlip (q : Qubit) : Unit { 
    body (...) {
        Z(q);
    }
    adjoint self;
}

Task 1.4* Amplitude change: \(\left| 0 \right>\) to \(cos(\theta)\left| 0 \right> + sin(\theta)\left| 1 \right>\)

Inputs: A qubit in state \(α \left| 0 \right> + β \left| 1 \right>\) and angle \(\theta\)

Goal: Change the state of the qubit as follows:

If the qubit is in state \(α \left| 0 \right>\) change its state to \(cos(\theta)\left| 0 \right> + sin(\theta)\left| 1 \right>\)

If the qubit is in state |1⟩, change its state to \(-sin(\theta)\left| 0 \right> + cos(\theta)\left| 1 \right>\)

Again, if you did go over the quantum quest notes, you will spot this is the result of rotation. However, in the lecture notes, it didn’t mention which axis the qubit was rotated around. After reading the docs, the Ry seems to be the correct gate since the matrix matches the amplitude value. Note, the angle we passed in needs to be double since Ry it divides the angle we passed in by two. If you are wondering why they divide the angle by two, please look up Bloch Sphere and how rotation is done on it.

operation AmplitudeChange (q : Qubit, alpha : Double) : Unit
is Adj {        
    Ry(alpha * 2.0, q);
}

Task 1.5 Phase flip

Input: A qubit in state \(β \left| 0 \right> + γ \left| 1 \right>\)

Goal: Change the qubit state to \(β \left| 0 \right> + iγ \left| 1 \right>\)

Going through each gate in the doc and match the matrix with the result amplitude will find S gate is the solution.

operation PhaseFlip (q : Qubit) : Unit 
is Adj {
    S(q);
}

Task 1.6* Phase change

Input: A qubit in state \(β \left| 0 \right> + γ \left| 1 \right>\) and Angle \(\alpha\)

Goal: Change the state of the qubit as follows:

If the qubit is in state \(\left| 0 \right>\), don’t change its state

If the qubit is in state \(\left| 1 \right>\), change its state to \(e^{i\alpha}\left| 1 \right>\)

Again, going through the doc and R1 gate is doing exactly this kata is asking.

operation PhaseChange (q : Qubit, alpha : Double) : Unit
is Adj {
    R1(alpha, q);
}

Task 1.7 Bell state change - 1

Input: Two entangled qubits in Bell state \(|Φ⁺⟩ = \frac{\left| 00 \right> + \left| 11 \right>}{\sqrt{2}}\)

Goal: Change the two-qubit state to \(|Φ⁻⟩ = \frac{\left| 00 \right> - \left| 11 \right>}{\sqrt{2}}\)

Transforming between bell state is an important prerequisite before understanding super dense coding. Kata 1.7 - 1.9 shows how we can transform from \(|Φ⁺⟩ = \frac{\left| 00 \right> + \left| 11 \right>}{\sqrt{2}}\) to other three bell states. For this one, the target state is \(|Φ⁻⟩ = \frac{\left| 00 \right> - \left| 11 \right>}{\sqrt{2}}\). This can be achieved by applying Z gate to the first qubit.

operation BellStateChange1 (qs : Qubit[]) : Unit
is Adj {
    Z(qs[0]);
}

Task 1.8 Bell state change - 2

Input: Two entangled qubits in Bell state \(|Φ⁺⟩ = \frac{\left| 00 \right> + \left| 11 \right>}{\sqrt{2}}\)

Goal: Change the two-qubit state to \(|Ψ⁺⟩ = \frac{\left| 01 \right> + \left| 10 \right>}{\sqrt{2}}\)

This can be achieved by applying X gate to the first qubit.

operation BellStateChange1 (qs : Qubit[]) : Unit
is Adj {
    X(qs[0]);
}

Task 1.9 Bell state change - 3

Input: Two entangled qubits in Bell state \(|Φ⁺⟩ = \frac{\left| 00 \right> + \left| 11 \right>}{\sqrt{2}}\)

Goal: Change the two-qubit state to \(|Ψ⁻⟩ = \frac{\left| 01 \right> - \left| 10 \right>}{\sqrt{2}}\)

This one is a little tricky, We can achieve the goal state by first applying X gate to transform the state to \(|Ψ⁺⟩ = \frac{\left| 01 \right> + \left| 10 \right>}{\sqrt{2}}\) then Z gate on first qubit to flip the sign.

operation BellStateChange1 (qs : Qubit[]) : Unit
is Adj {
    X(qs[0]);
    Z(qs[0]);
}

Super dense coding allows quantum computers to transfer 2 classic bits information with only one qubit. You can read more at demystifying superdense coding. It also explains how to transform between bell states which is the solution of 1.7 - 1.9.

Part II. Multi-Qubit Gates

Task 2.1 Two-qubit gate - 1

Input: Two unentangled qubits:

The first qubit will be in state \(α \left| 0 \right> + β \left| 1 \right>\), the second - in state \(\left| 0 \right>\)

Goal: Change the two-qubit state to \(α \left| 00 \right> + β \left| 11 \right>\)

Typical use case of CNOT gate.

operation TwoQubitGate1 (qs : Qubit[]) : Unit {
    body (...) {
        CNOT(qs[0], qs[1]);
    }
    adjoint self;
}

Task 2.2 Two-qubit gate - 2

Input: Two qubits in state \(\frac{\left| 00 \right> + \left| 01 \right> + \left| 10 \right> + \left| 11 \right>}{2}\)

Goal: Change the two-qubit state to \(\frac{\left| 00 \right> + \left| 01 \right> + \left| 10 \right> - \left| 11 \right>}{2}\)

We only need to flip the sign of the last state and already know this can be achieved by Z gate. To complete this kata, we need some extra conditional check on the first bit, so the gate we need is a Controlled-Z gate and luckily Q# provides CZ directly.

operation TwoQubitGate2 (qs : Qubit[]) : Unit {
    body (...) {
        CZ(qs[0], qs[1]);
    }
    adjoint self;
}

Task 2.3 Two-qubit gate - 3

Input: Two qubits in state \(\frac{\alpha\left| 00 \right> + \beta\left| 01 \right> + \gamma\left| 10 \right> + \delta\left| 11 \right>}{2}\)

Goal: Change the two-qubit state to \(\frac{\alpha\left| 00 \right> + \beta\left| 10 \right> + \gamma\left| 01 \right> + \delta\left| 11 \right>}{2}\)

This task ask us to swap the state between a pair of qubits. Q# does have a SWAP gate, however, the kata also ask us to solve it without using SWAP. I started by thinking how to transform from \(\left| 01 \right>\) to \(\left| 10 \right>\), which is:

CNOT(qs[1], qs[0]);
CNOT(qs[0], qs[1]);

Then adding extra gate to fulfill the two lefted cases. My final solution is:

operation TwoQubitGate3 (qs : Qubit[]) : Unit {
    body (...) {
        CNOT(qs[1], qs[0]);
        CNOT(qs[0], qs[1]);
        CNOT(qs[1], qs[0]);
    }
    adjoint self;
}

Task 2.4 Toffoli gate

Input: Three qubits in an arbitrary three-qubit state \(\alpha\left| 000 \right> + \beta\left| 001 \right> + \gamma\left| 010 \right> + \delta\left| 011 \right> + \epsilon\left| 100 \right> + \zeta\left| 101 \right> + \eta\left| 110 \right> + \theta\left| 111 \right>\)

Goal: Flip the state of the third qubit if the state of the first two is \(\left| 11 \right>\): i.e., change the three-qubit state to: \(\alpha\left| 000 \right> + \beta\left| 001 \right> + \gamma\left| 010 \right> + \delta\left| 011 \right> + \epsilon\left| 100 \right> + \zeta\left| 101 \right> + \eta\left| 111 \right> + \theta\left| 110 \right>\)

Famous Toffoli gate. Q# named it CCNOT.

operation ToffoliGate (qs : Qubit[]) : Unit {
    body (...) {
        CCNOT(qs[0], qs[1], qs[2]);
    }
    adjoint self;
}

Task 2.5 Fredkin gate

Input: Three qubits in an arbitrary three-qubit state \(\alpha\left| 000 \right> + \beta\left| 001 \right> + \gamma\left| 010 \right> + \delta\left| 011 \right> + \epsilon\left| 100 \right> + \zeta\left| 101 \right> + \eta\left| 110 \right> + \theta\left| 111 \right>\)

Goal: Swap the states of second and third qubit if and only if the state of the first qubit is \(\left| 1 \right>\): \(\alpha\left| 000 \right> + \beta\left| 001 \right> + \gamma\left| 010 \right> + \delta\left| 011 \right> + \epsilon\left| 100 \right> + \zeta\left| 110 \right> + \eta\left| 101 \right> + \theta\left| 111 \right>\)

I spent quite a lot of time on this one. Then I realized, this is just the swap gate in question 2.3 with a controlled bit set to the first qubit. This kata can be solved with three Tofolli gate. I then simplified the solution to use two CNOT gate as the first and last CCNOT can be reduced to CNOT. I found it is easier to understand with below image. The red square is the swap circuit.

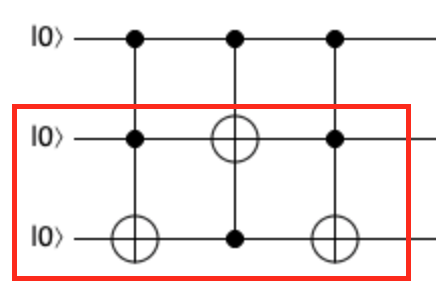
operation FredkinGate (qs : Qubit[]) : Unit {
    body (...) {
        // CCNOT(qs[0], qs[1], qs[2]);
        // CCNOT(qs[0], qs[2], qs[1]);
        // CCNOT(qs[0], qs[1], qs[2]);

        CNOT(qs[1], qs[2]);
        CCNOT(qs[0], qs[2], qs[1]);
        CNOT(qs[1], qs[2]);
    }
    adjoint self;
}

Conclusion

This first set of katas introduced some basic gates of quantum computing. There are not a lot of thinking through this exercises as most of them is just finding the right gate to use. In the following sets, there will be more and more thinking involved base on the knowledge we gained here.