量子電腦系列:量子力學真的能做到瞬間移動嗎?
19 Jul 2020從七龍珠的悟空到各種遊戲裡的閃現,瞬間移動這種夢幻般的技能相信大家都很熟悉。但你知道在現實生活中,我們已經可以利用量子力學來做到類似的效果而且有成功的實驗了嗎?這篇文章的目的就是帶大家了解瞬間移動背後的理論與計算。
如果對量子電腦不是很熟的讀者,歡迎讀一下 淺談量子電腦 增加對量子比特 (Qubit) 的一些認識,讀起本文也會更順暢一點喔。
定義
在我們開始之前,我們需要定義本篇文章指的瞬間移動是什麼。正確的來說是叫量子傳送 (Quantum Teleportation),是一個把量子比特的狀態傳送到遠處另一個量子比特上的技術。由於傳送前後的量子比特之間沒有任何連結,因此產生出資訊瞬間移動的效果。順帶一提,相對論並沒有被打破,量子傳輸的速度還是受限於光速。
你可能覺得傳輸資訊沒什麼了不起的,我們現在天天在網路上傳送大量的訊息。但在量子比特所處的微觀世界中,「觀測」是一個會破壞訊息的行為。也就是說,在傳送前我們無法得知傳送的內容。有點像是我家有杯水,我要在不知道杯子裡有多少水的前提下,讓這些水移動到你家裡的空杯子裡,而且我的杯子無法被帶到你家。
接下來我們用嚴謹一點的數學來定義我們即將要傳送的量子比特。這個量子比特的狀態一般來說都是未知的,用數學來表示就是:
\[\left| \psi \right> = \alpha \left| 0 \right> + \beta \left| 1 \right>\]\(\alpha^2\) 和 \(\beta^2\) 分別表示量子比特測量後結果為 0 和 1 的可能性。所以透過這兩個變數可以包含單個量子比特的所有可能狀態。
在傳送過程中,我們不用也無法知道 \(\alpha\) 和 \(\beta\) 的數值,但這其實不影響傳送,我們只要確保傳送前後這兩個數值沒有改變就算成功了。\(\alpha\) 和 \(\beta\) 就是我們要傳送的資訊。一旦它們改變,代表這個量子比特的狀態與傳送前不同,也意味著傳送失敗。
量子閘
接下來,我們快速介紹一些傳送會需要用到的量子閘 (Quantum Gate)。量子閘與電腦裡的邏輯閘很類似,它們是用來改變量子比特狀態的閘門。
X閘 (X Gate)
X gate 相當於邏輯閘的「非」門。下圖是 X gate 的真值表,每一行表示當這個閘門的輸入是左列的數值的話,輸出就是右列的值。例如把 \(\left| 0 \right>\) 輸入給 X gate,輸出就會是 \(\left| 1 \right>\) 。你也可以把它們想像成類似販賣機的機器,丟個零錢進去,換個飲料出來。
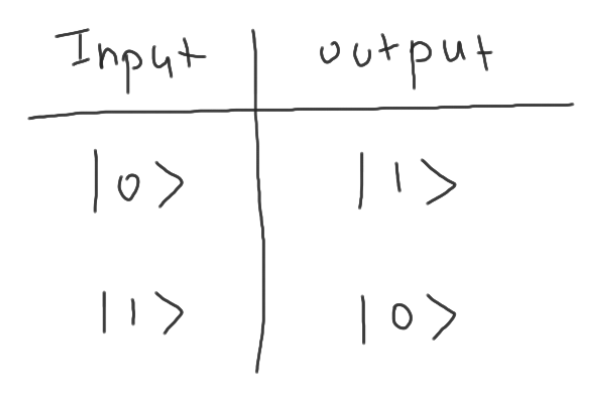
線路圖表示:
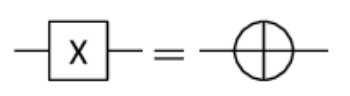
X gate 有兩種表示法,右邊的形式比較常出現在等等會提到的 CNOT gate。
H閘 (Hadamard Gate)
Hadamard gate 又稱 H gate。H gate 在量子演算法裡被大量地被運用,原因是它可以把一個在非疊加態的量子比特例如 \(\left| 0 \right>\) 轉換成疊加態。 H gate 同時也是產生糾纏態 (Entanglement) 線路的必要零件。以下是它的真值表:
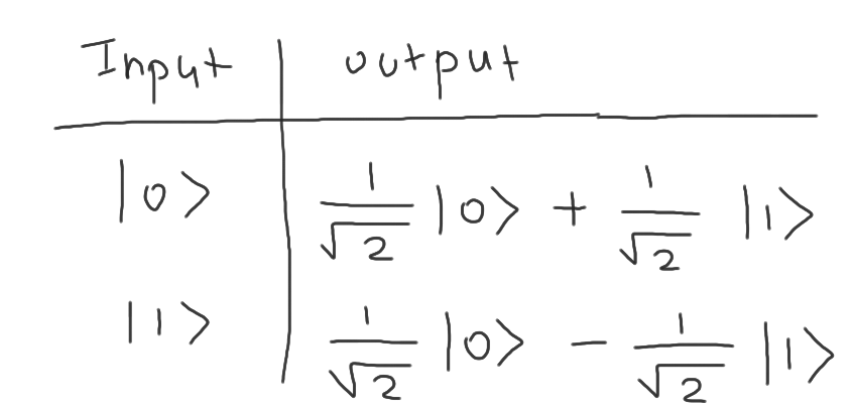
線路圖表示:
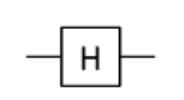
Z閘 (Z Gate)
當輸入為 \(\left| 1 \right>\) 時,Z gate 會改變正負號。真值表:
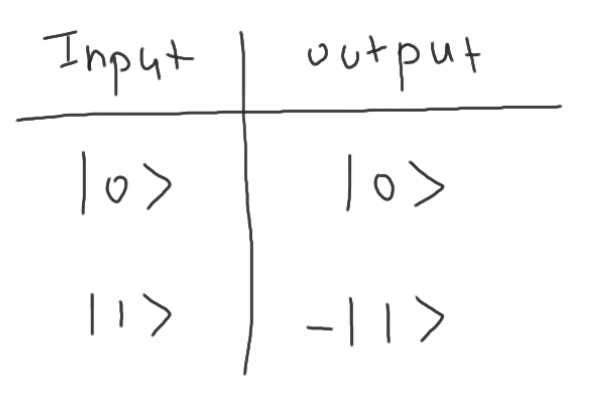
線路圖表示:
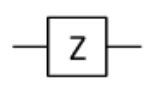
前面提到的量子閘輸入都是一個量子比特。接下來要介紹的是兩個輸入的量子閘。
CNOT閘 (Controlled-Not Gate 或 CNOT Gate)
這邊把線路圖放到前面,解釋起來比較清楚:
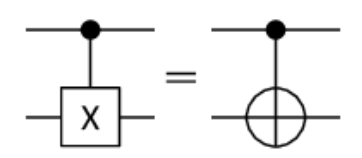
CNOT gate 有兩個輸入,第一個輸入是圖中 X gate 的開關,第二個輸入則是會通過 X gate。這個 X gate 會根據第一個量子比特輸入的數值來決定要不要作用。只有當第一個輸入是 \(\left| 1 \right>\) 時,X gate 才會起作用。
真值表:
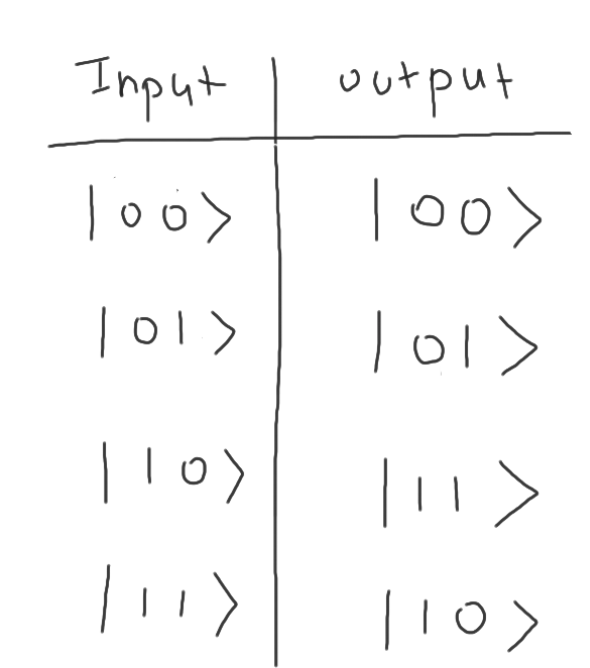
可以看到當第一個量子比特是 \(\left| 0 \right>\) 時,第二個量子比特並沒有被反轉,相當於 X gate 不存在。但當第一個量子比特是 \(\left| 1 \right>\) 時,X gate 就發揮作用了。
CZ閘 (Controlled-Z Gate 或 CZ Gate)
CZ 和 CNOT 類似,只是把 X gate 換成 Z gate。
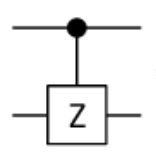
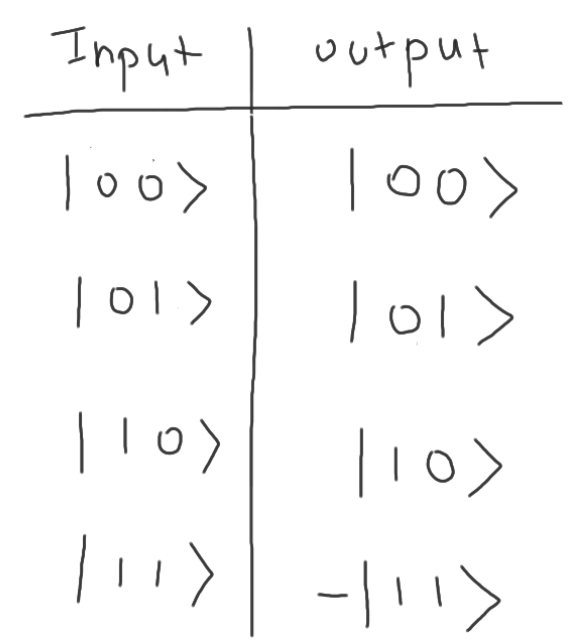
真值表:
測量 (Measurement)
測量在量子線路裡有著破壞性的後果,一旦量子比特被測量,它就會崩塌到 0 或 1 其中一個狀態。這樣講可能有點難懂,這時我們就要請出物理學四大神獸之一的薛丁格的貓。在這個思想實驗裡,我們在一個盒子中放入毒氣與貓,在我們打開盒子之前並不知道貓是生是死 (貓處於疊加態)。一但盒子被打開,貓的狀態 (死活) 就被確定了也就是前面提到的崩塌 (疊加態的崩塌)。在線路圖裡,測量的表示為:
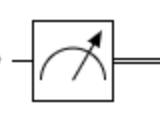
這邊值得注意的小細節是過了測量後,線從一條變成了兩條。這代表量子比特已經崩塌,作用已退化成一般電腦用的位元 (bit)。
不可克隆原理 (No-cloning theorem)
不可克隆原理指的是我們無法建構出一個量子線路來複製一個未知狀態的量子比特。各位有興趣可以去看數學證明。量子傳送的初衷就是將一個未知狀態的量子比特從 A 點送到 B 點,而如果複製是可行的話,我們也就不用大費周章的傳送,只需要在目的地將目標複製出來就行了。也正是因為這個限制,才有了量子傳送的發明。
量子傳送
前面花了很多篇幅把先備知識交代完,總算可以進入正題了。我會先試著用文字的方式大概描述傳送的過程,接著再帶著各位配合量子線路一步步做計算,用數學的形式理解量子傳輸。
量子傳輸需要用到三個量子比特,我們稱它們為 A,B 和 C。A 是要傳送的量子比特,我們並不知道它的狀態。B 和 C 我們可以準備兩個在 \(\left| 0 \right>\) 狀態的量子比特。接著把 B 和 C 送進量子糾纏線路讓它們進入量子糾纏的狀態。完成之後我們可以把 B 留在出發地,C 帶到目的地。理論上這兩個量子比特之間的距離可以是任意長度,資源許可的話,把目的地設在其他星球上也不是問題。一旦 C 就位後,我們就準備好做傳送了。在出發地把 A 和 B 送入量子傳送線路,線路會輸出兩個位元 (bit)。最後把這兩個位元送到目的地並根據它們的數值把 C 調整到 A 的狀態就算傳輸成功。看完如果滿頭問號的話沒關係,這邊是給一個大方向,接下來會一步一步解釋。
從上面的步驟可以看出 A 和 C 在整個傳輸階段沒有任何連結,一但技術成熟,未來可以想見有企業會專門準備大量地 B 和 C 在世界各地方便資訊傳送。另一個值得注意的地方是我們還是需要傳送兩個傳統的位元,這代表傳送的速度還是無法超過光速。最後由於 A 和 B 在通過量子傳送線路時會被測量並產生兩個傳統位元,A 不再保有原本的狀態並符合不可克隆原理。
量子傳送線路圖
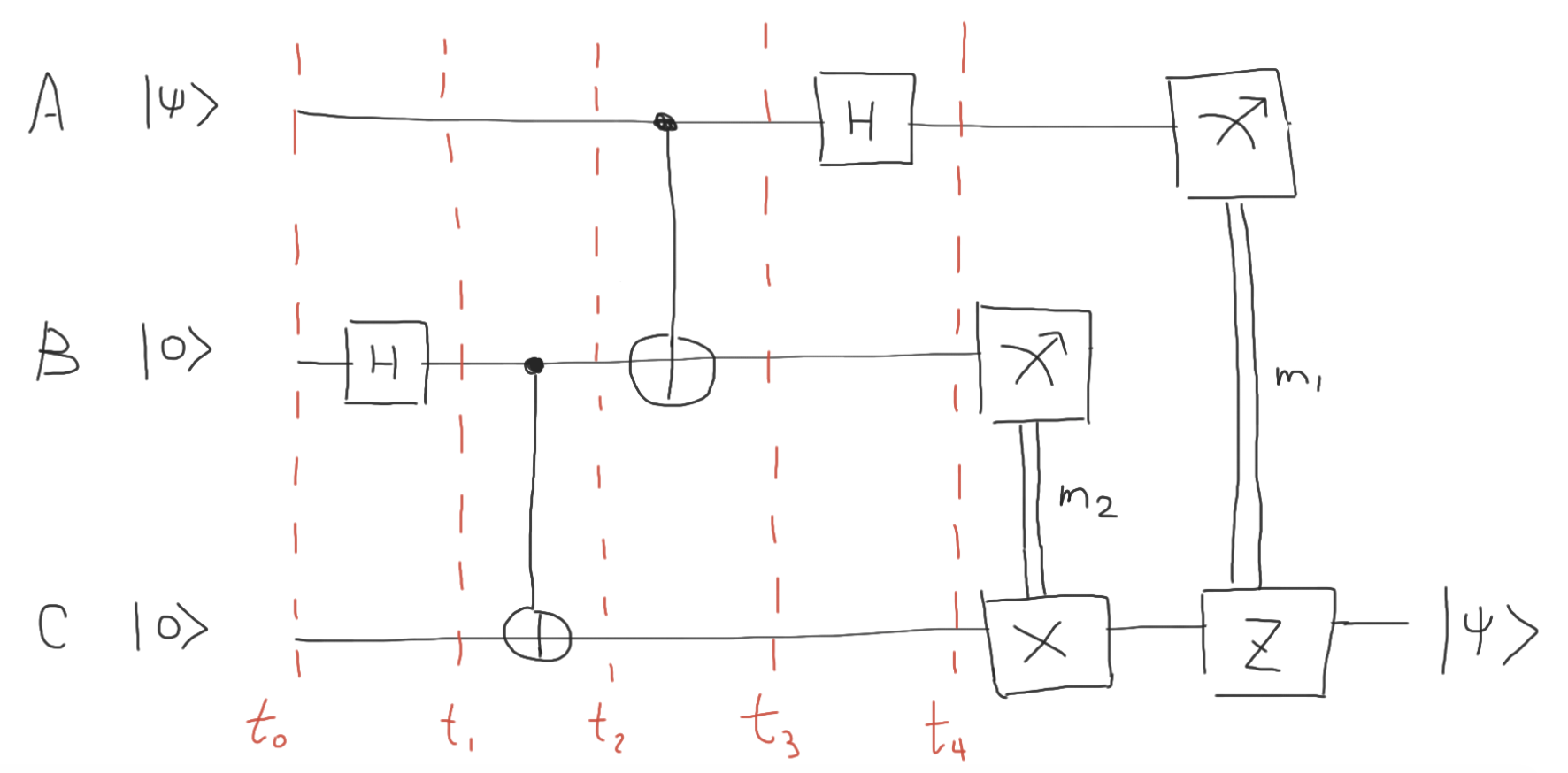
接下來我們會用數學來解釋量子傳送並展示出這三個量子比特在不同時間點的狀態。圖中 m1 代表的是 A 的測量結果,m2 是 B 的測量結果。
起始狀態 (\(t_{0}\)):
我們的起始狀態是由:
A: \(\left| \psi \right> = \alpha \left| 0 \right> + \beta \left| 1 \right>\)
B: \(\left| 0 \right>\)
C: \(\left| 0 \right>\)
所組成。
多個量子比特的組合在數學是使用張量積 (tensor product),例如兩個 \(\left| 0 \right>\) 可以寫成下面三種型態:
\[\left| 0 \right> \otimes \left| 0 \right> = \left| 0 \right>\left| 0 \right> = \left| 00 \right>\]因此,初始狀態數學表示如下:
\[t_{0}: (\alpha \left| 0 \right> + \beta \left| 1 \right>) \otimes \left| 0 \right> \otimes \left| 0 \right> = \alpha \left| 000 \right> + \beta \left| 100 \right>\]量子糾纏線路 (\(t_{0}\) ~ \(t_{2}\)):
\(t_{0}\) ~ \(t_{2}\) 的這段線路主要是用來讓 B 和 C 進入量子糾纏狀態。經過任何量子閘時,我們要對所有的狀態進行計算。在進入 H Gate 之前,三個量子比特有兩個狀態,分別是 \(\alpha \left| 000 \right>\) 和 \(\beta \left| 100 \right>\) 。 由於只有 B 通過量子閘,轉換只會發生在第二個量子比特。透過之前的 H gate 真值表,我們可以算出在 \(t_{1}\) 時的狀態。
\[t_{1}: \alpha \left| 0 \right> H(\left| 0 \right>) \left| 0 \right> + \beta \left| 1 \right> H(\left| 0 \right>) \left| 0 \right>\] \[t_{1}: \frac{\alpha}{\sqrt{2}} \left| 0 \right> (\left| 0 \right> + \left| 1 \right>) \left| 0 \right> + \frac{\beta}{\sqrt{2}} \left| 1 \right> (\left| 0 \right> + \left| 1 \right>) \left| 0 \right>\] \[t_{1}: \frac{\alpha}{\sqrt{2}} \left| 000 \right> + \frac{\alpha}{\sqrt{2}} \left| 010 \right> + \frac{\beta}{\sqrt{2}} \left| 100 \right> + \frac{\beta}{\sqrt{2}} \left| 110 \right>\]\(t_{1}\) 和 \(t_{2}\) 之間有作用於 B 和 C 的 CNOT gate,控制點在 B。換句話說,只有當第二個量子比特的狀態是 \(\left| 1 \right>\) 時,我們才需要反轉第三個量子比特。
\[t_{2}: \frac{\alpha}{\sqrt{2}} \left| 000 \right> + \frac{\alpha}{\sqrt{2}} \left| 011 \right> + \frac{\beta}{\sqrt{2}} \left| 100 \right> + \frac{\beta}{\sqrt{2}} \left| 111 \right>\]這段線路和 A 完全沒有關係,是可以在傳送前事先準備的。在 \(t_{2}\) 後,C 就可以被帶到傳送目的地了。
出發地傳送線路 (\(t_{2}\) ~ \(t_{4}\)):
\(t_{2}\) 和 \(t_{3}\) 之間也是 CNOT,只是換成了 A 和 B。
\[t_{3}: \frac{\alpha}{\sqrt{2}} \left| 000 \right> + \frac{\alpha}{\sqrt{2}} \left| 011 \right> + \frac{\beta}{\sqrt{2}} \left| 110 \right> + \frac{\beta}{\sqrt{2}} \left| 101 \right>\]\(t_{4}\) 則是 A 過了 H gate。值得注意的是 \(\frac{\alpha}{\sqrt{2}}\) 變成了 \(\frac{\alpha}{2}\),因為 H gate 會為等式帶來一個 \(\frac{1}{\sqrt{2}}\)。
\[t_{4}: \frac{\alpha}{\sqrt{2}} H(\left| 0 \right>)\left| 00 \right> + \frac{\alpha}{\sqrt{2}} H(\left| 0 \right>)\left| 11 \right> + \frac{\beta}{\sqrt{2}} H(\left| 1 \right>)\left| 10 \right> + \frac{\beta}{\sqrt{2}} H(\left| 1 \right>) \left| 01 \right>\] \[t_{4}: \frac{\alpha}{2} (\left| 0 \right> + \left| 1 \right>) \left| 00 \right> + \frac{\alpha}{2} (\left| 0 \right> + \left| 1 \right>) \left| 11 \right> + \frac{\beta}{2} (\left| 0 \right> - \left| 1 \right>) \left| 10 \right> + \frac{\beta}{2} (\left| 0 \right> - \left| 1 \right>) \left| 01 \right>\]就在這個時間點,我們可以重新思考一下傳送成功的條件:把在出發地的 A 的狀態轉移到在目的地的 C 上。也就是讓 C 的狀態成為 \(\alpha \left| 0 \right> + \beta \left| 1 \right>\) 。讓我們試試看整理 \(t_{4}\) 的狀態把 \({\alpha}\) 和 \({\beta}\) 整理到第三個量子比特上:
先把括號展開:
\[t_{4}: \frac{\alpha}{2} \left| 000 \right> + \frac{\alpha}{2} \left| 100 \right> + \frac{\alpha}{2} \left| 011 \right> + \frac{\alpha}{2} \left| 111 \right> + \frac{\beta}{2} \left| 010 \right> - \frac{\beta}{2} \left| 110 \right> + \frac{\beta}{2} \left| 001 \right> - \frac{\beta}{2} \left| 101 \right>\]重新排列:
\[t_{4}: \frac{\alpha}{2} \left| 000 \right> + \frac{\beta}{2} \left| 001 \right> + \frac{\alpha}{2} \left| 011 \right> + \frac{\beta}{2} \left| 010 \right> + \frac{\alpha}{2} \left| 100 \right> - \frac{\beta}{2} \left| 101 \right> + \frac{\alpha}{2} \left| 111 \right> - \frac{\beta}{2} \left| 110 \right>\]把 C 獨立出來:
\[t_{4}: \frac{1}{2} \left| 00 \right> (\alpha \left| 0 \right> + \beta \left| 1 \right>) + \frac{1}{2} \left| 01 \right> (\alpha \left| 1 \right> + \beta \left| 0 \right>) + \frac{1}{2} \left| 10 \right> (\alpha \left| 0 \right> - \beta \left| 1 \right>) + \frac{1}{2} \left| 11 \right> (\alpha \left| 1 \right> - \beta \left| 0 \right>)\]整理完可以發現在 \(t_{4}\) 時只對 A 和 B 做測量的話會有四種可能的狀態,分別為:
第一種:A 和 B 都是 0,C 的狀態是 \(\alpha \left| 0 \right> + \beta \left| 1 \right>\)
第二種:A 是 0,B 是 1,C 的狀態是 \(\alpha \left| 1 \right> + \beta \left| 0 \right>\)
第三種:A 是 1,B 是 0,C 的狀態是 \(\alpha \left| 0 \right> - \beta \left| 1 \right>\)
第四種:A 和 B 都是 1,C 的狀態是 \(\alpha \left| 1 \right> - \beta \left| 0 \right>\)
我們再回頭看一次成功傳送的條件:讓 C 的狀態成為 \(\alpha \left| 0 \right> + \beta \left| 1 \right>\) 。
有沒有發現第一種測量結果達到了我們傳輸成功的條件 🤩!但是,在量子計算的世界裡,不可能每次測量都碰到第一種結果。想要確保 100% 的成功率,我們需要根據 A 和 B 的測量結果把 C 的狀態調整到 \(\alpha \left| 0 \right> + \beta \left| 1 \right>\) 。所以傳送的下一步就是把 A 和 B 的測量結果送到 C 所在的目的地。
出發地傳送線路 (\(t_{4}\) 之後):

這邊再貼一次線路圖方便對比並分別對四種可能狀態進行分析:
A = 0, B = 0
C 的狀態: \(\alpha \left| 0 \right> + \beta \left| 1 \right>\)
這是剛剛看到的第一種測量結果,我們不用對 C 做任何調整傳送就成功了。
A = 0, B = 1
C 的狀態: \(\alpha \left| 1 \right> + \beta \left| 0 \right>\)
與目標差別在於 \(\left| 0 \right>\) 和 \(\left| 1 \right>\) 反了。這裡可以簡單地讓 C 過一下 X gate 就能把狀態調整成目標狀態。
\[X(\alpha \left| 1 \right> + \beta \left| 0 \right>) = \alpha X(\left| 1 \right>) + \beta X(\left| 0 \right>) = \alpha \left| 0 \right> + \beta \left| 1 \right>\]在線路圖裡也可以看到 X gate 是被 B 的測量結果所控制:當 B 是 1 時,X gate 才會對 C 起作用。
A = 1, B = 0
C 的狀態: \(\alpha \left| 0 \right> - \beta \left| 1 \right>\)
這邊 \(\left| 1 \right>\) 的正負號錯了。不過!之前提到的 Z gate 正好可以幫我們修正。
\[Z(\alpha \left| 0 \right> - \beta \left| 1 \right>) = \alpha Z(\left| 0 \right>) - \beta Z(\left| 1 \right>) = \alpha \left| 0 \right> + \beta \left| 1 \right>\]A = 1, B = 1
C 的狀態: \(\alpha \left| 1 \right> - \beta \left| 0 \right>\)
這個組合與目標狀態相差的最多,但透過 X 和 Z gate 也能輕鬆解決。首先,先過一下 X gate:
\[X(\alpha \left| 1 \right> - \beta \left| 0 \right>) = \alpha X(\left| 1 \right>) - \beta X(\left| 0 \right>) = \alpha \left| 0 \right> - \beta \left| 1 \right>\]過完 X gate 後的狀態就與 A = 1, B = 0 時的 C 狀態相同了,只需要再過一個 Z gate 就可以調整成目標狀態。
現在不管在出發地測量出哪種結果,我們都能夠在 C 上面重現 A 的狀態了!
現實中的實現
看到這裡的大家可能都很好奇,既然理論上證明可行了,那在真實世界中有成功過嗎?答案是有的,目前成功傳輸的最大距離是 1400 公里。其中最大的限制在於量子比特的穩定性,這同時也是量子電腦發展的主要瓶頸之一。
量子比特是一個抽象概念,就像我們透過電壓超過一定伏特來判定位元的 1 與 0,我們也可以透過各種物理性質來實現量子比特,例如:光子的偏振,電子的自旋等。而人體也是由粒子所組成,這不禁讓人想像,在遙遠的未來,人是否能夠以粒子為單位做類似的傳送。
最後,用個哲學問題來為這篇過硬文章做結尾:量子傳送是將原本粒子的狀態傳送到新的粒子上,以人當例子的話,相當於在目的地有一副新的身軀只是狀態與傳送前相同。這時,你認為傳送前後的人還是同一個人嗎?
