機器學習基石-第二講筆記

24 Feb 2016

前言

最近想透過 Coursera 上的機器學習基石課程來了解一直都很夯的機器學習，但由於自大學以來就很少再碰數學的關係，在第二講討論感知學習演算法時就開始卡關。在多次問候 Google 大神後總算是有了基本的了解，於是想藉由文章記錄學習的過程。

註：本篇文章所有圖片都是來自課程投影片。

感知學習演算法

感知學習演算法又簡稱 PLA 。 PLA 可以用在能完全二分的問題中，像是該不該發信用卡給某個人或是某個學生是否可以畢業等等。在 PLA 中，我們會針對每種特徵值計算一個權重，當所有的特徵值乘上相對的權重加起來大於某個設定的門檻時，就會回傳是，反之則否。

課程中提到的例子為是否該發信用卡給某個人。在這個例子當中，這個人的年齡，年薪，欠債等等資料都是特徵值。而此演算法則會在判斷錯誤 (輸入資料說該發但算出來的結果說不該發) 時修改每項特徵值的權重，直到每項資料都能正確回答時才會停止。

基本的公式為：

圖中 x 代表著特徵值，而 w 是相對於特徵值的權重。

如果使用簡單的資料，我們可以視覺化整個過程。 在二維 (2D) 的世界中，運作起來會像下圖：

碰到的問題

接下來的部分會比較偏重於數學以及我個人遇到的問題，想要對 PLA 有更深的了解的話歡迎前往Coursera觀看課程影片。如果你有在課程中遇到數學的問題的話或許可以參考以下內容，說不定能解決一些疑慮。

如何調整權重 (w)

課程裡提到了如何自動調整權重，也給了相對應的公式：

\[\begin{align*} w_{t+1} \leftarrow w_t + y_{n(t)} x_{n(t)} \\ \text{判斷錯誤時: } sign(w_t^Tx_{n(t)}) \neq y_{n(t)} \end{align*}\]

但我很好奇為什麼這樣就能把 w 自動調整到我們所期望的值呢？由於課程中一再的提到向量內積，於是經過一番查證後發現了一套公式，也幫助了我思考接下來的幾個問題：

\[w \cdot x = w^T x = \lvert\overrightarrow w\rvert\lvert\overrightarrow x\rvert\cos(\theta)\]

\(\lvert\overrightarrow w\rvert\) 是 w 這個向量的長度，而 \(\theta\) 則是 w 與 x 之間的夾角。由於向量的長度不會為負數，因此影響 \(w^Tx\) 是正還是負的主要因子就是 \(\theta\) 了。 \(\cos(\theta)\) 的特性是當 \(\theta\) 在 \(0^\circ\) 與 \(90^\circ\) 之間時是正數，在 \(90^\circ\) 與 \(180^\circ\) 度之間時是負數。透過將 \(w_{t+1}\) 設為 w 與 x 兩個向量相加能夠縮小 \(w_{t+1}\) 與 x 之間的夾角進而使結果趨於正數，反之亦然。而根據公式，這個該加還是該減就取決於 \(y_{n(t)}\) 囉。

舉個例子：某次學習錯誤將原本結果該為 \(-1\) 的 \(y_{n(t)}\) 誤判成 \(+1\)，這代表 w 與 x 之間的角度太小，所以我們透過 \(w_{t+1} \leftarrow w_t + (-1) x_{n(t)} \) 來將夾角加大，使未來學習到這點時能正確的判斷成 \(-1\)。

為什麼分割線是垂直於 w

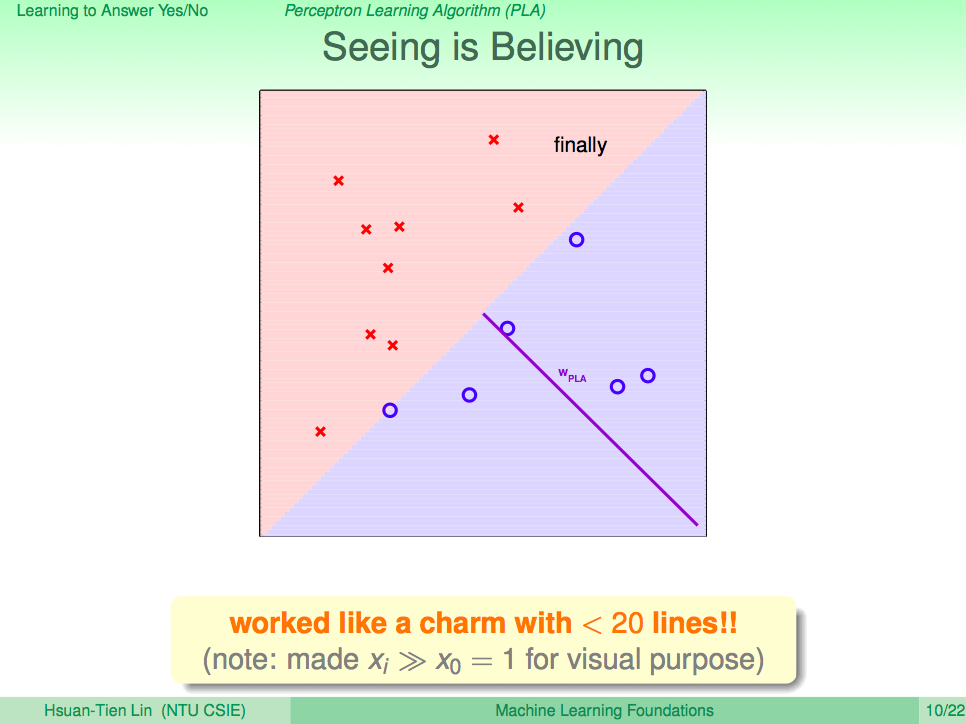
在上課時看到上圖就一直很好奇為什麼分割線與 w 垂直。但仔細想想後，其實這是一個理所當然的結果。我們再來看看剛剛提到的公式：

\[w \cdot x = w^T x = \lvert\overrightarrow w\rvert\lvert\overrightarrow x\rvert\cos(\theta)\]

當 w 與 x 的夾角 \(\theta\) 小於 \(90^\circ\) 時結果為正 (圖中的圈圈)，大於 \(90^\circ\) 時結果為負 (圖中的叉叉)。因此與夾角垂直的線自然就成了正與負的分水嶺囉。

證明 PLA 會停止

想要證明 PLA 會在不斷學習後停止，必須要有一個前提就是輸入資料能被完全二分化。另外就是投影片中提到的兩項證明。 下圖告訴了我們隨著修正的次數增加，\(w_f\) 與 \(w_t\) 之間的夾角會漸漸縮小。

但我們可以從 \(w^T x = \lvert\overrightarrow w\rvert\lvert\overrightarrow x\rvert\cos(\theta)\) 得知 \(w_f^T w_t\) 的結果會變大的原因不一定只有夾角縮小而已，也有可能是向量長度變大所導致。而以下這張圖告知了我們\(w_t\) 的成長是有限的。

接下來我們就可以利用以上來完成課程中沒提到的證明：

首先我們使用本段落第一張圖裡的公式 \(w_f^Tw_{t+1} \ge w_f^Tw_{t} + min_ny_nw_f^Tx_n\) 來推論 X 次更新後的樣子。這裡使用 X 而不是使用 T 的原因是因為不想讓 T 與向量轉置 (vector transpose) 的 T 混淆。

\[\begin{align} w_f^Tw_{X} &\ge w_f^Tw_{X-1} + min_ny_nw_f^Tx_n \\ &\ge w_f^Tw_0 + X * min_ny_nw_f^Tx_n \\ &= X * min_ny_nw_f^Tx_n \end{align}\]

接著利用本段落第二張圖中的 \(\lvert w_{t+1}\rvert^2 \le \lvert w_{t}\rvert^2 + max_n\lvert x_n\rvert^2\) 來推導以下公式：

\[\begin{align} \lvert w_{X}\rvert^2 &\le \lvert w_{X-1}\rvert^2 + max_n\lvert x_n\rvert^2 \\ &\le \lvert w_{0}\rvert^2 + X * max_n\lvert x_n\rvert^2 \\ &\le X * max_n\lvert x_n\rvert^2 \end{align}\]

在得到上述兩項公式後把他們帶入課程中提到的 \(\frac{w_f}{\lvert w_{f}\rvert} \frac{w_X}{\lvert w_{X}\rvert}\) (這裡一樣是用 X 取代 T):

\[\begin{align} \frac{w_f^T}{\lvert w_{f}\rvert} \frac{w_X}{\lvert w_{X}\rvert} &\ge \frac{X * min_ny_nw_f^Tx_n}{\lvert w_{f}\rvert \lvert w_{X}\rvert} \\ &\ge \frac{X * min_ny_nw_f^Tx_n}{\lvert w_{f}\rvert \sqrt X * max_n\lvert x_n\rvert} \\ &= \sqrt X * \frac{min_ny_nw_f^Tx_n}{\lvert w_{f}\rvert * max_n\lvert x_n\rvert} \end{align}\]

這樣也就得出了投影片中最後的方程式。理解了以上之後，第二講中的第三題也就自然不難懂了。以下是題目：

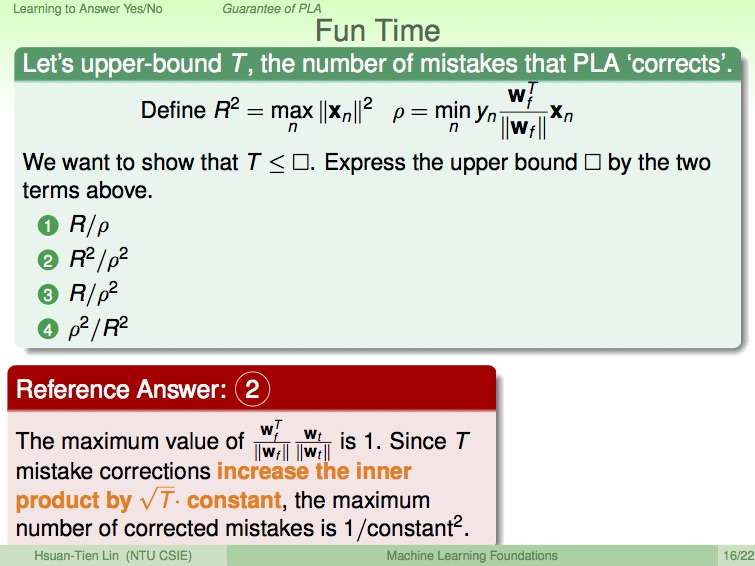
因為 \(w_f\) 與 \(w_X\) 已經被正規化 (Normalized)，因此長度都為 1。因此 \(\frac{w_f}{\lvert w_{f}\rvert} \frac{w_X}{\lvert w_{X}\rvert}\) 的結果最大就是 1 了 (當夾角為 0 時)。 我們同時可以把問題中的 \(R\) 與 \(\rho\) 帶入剛剛導出的公式得知：

\[1 \ge \sqrt T * \frac{\rho}{R}\]

這樣就能得到答案 \(T \le \frac{R^2}{\rho^2}\)囉。

Pocket Algorithm

PLA 要能解決問題必須有一個很大的前提，就是輸入資料能夠被完整的分成兩部分 (分黑即白)，不然 PLA 會不斷偵測到錯誤而無法停下。在資料無法被完整的二分化時，我們可以透過 Pocket Algorithm 來達到比較好的結果 (非完美) 同時能使演算法停止。

簡單來說，就是在每一次取得新的權重 (w) 時，如果發現比之前的結果更好，就記錄下來。當我們設定學習的迴圈次數到達時，演算法就會將所記錄的最好結果給返回。